PCA מחשבת את הווקטורים העצמיים של מטריצת המשתנות ("הצירים העיקריים") וממיינת אותם לפי הערכים העצמיים שלהם (כמות השונות המוסברת). לאחר מכן ניתן להקרין את הנתונים המרוכזים על צירים עיקריים אלה כדי להניב רכיבים עיקריים ("ציונים"). לצורך הפחתת מימדיות, ניתן לשמור רק קבוצת משנה של מרכיבים עיקריים ולזרוק את השאר. (עיין כאן ב מבוא הדיוט ל- PCA.)

תן ל- $ \ mathbf X_ \ text {raw} $ להיות $ n \ פעמים p מטריצת $ $ עם $ n $ שורות (נקודות נתונים) ו- $ p $ עמודות (משתנים או תכונות). לאחר חיסור הווקטור הממוצע $ \ boldsymbol \ mu $ מכל שורה, נקבל את מטריצת הנתונים מרוכזת $ \ mathbf X $. תן ל- $ \ mathbf V $ להיות מטריצת $ p \ times k $ של כמה $ k $ ווקטורים עצמיים שבהם אנו רוצים להשתמש; לרוב אלה הם הווקטורים העצמיים $ k $ עם הערכים העצמיים הגדולים ביותר. ואז המטריצה ​​$ n \ times k $ של תחזיות PCA ("ציונים") תינתן בפשטות על ידי $ \ mathbf Z = \ mathbf {XV} $.

זה מודגם באיור שלמטה: עלילת המשנה הראשונה מציגה נתונים מרוכזים (אותם נתונים בהם אני משתמש ב האנימציות שלי בשרשור המקושר) ואת התחזיות שלה על הציר הראשי הראשון. עלילת המשנה השנייה מציגה רק את ערכי ההקרנה הזו; המימד הצטמצם משניים לאחד:

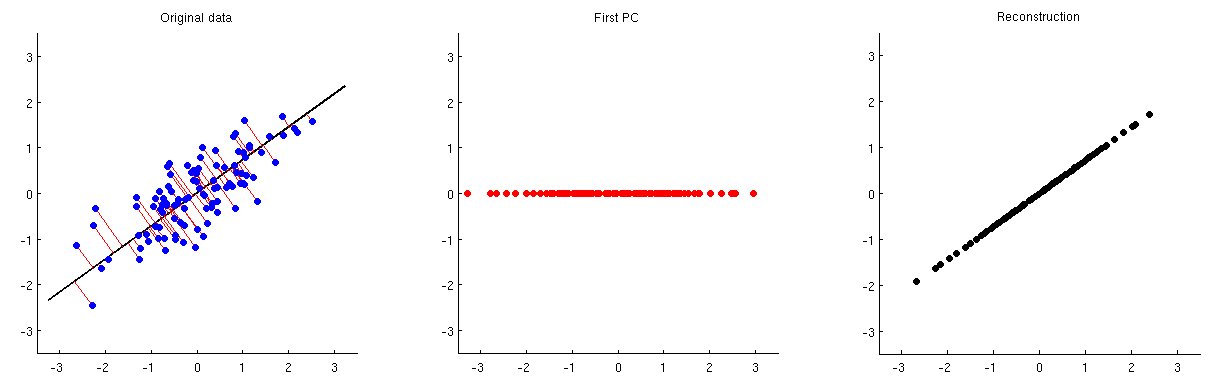
על מנת להיות מסוגל לשחזר את שני המשתנים המקוריים ממרכיב עיקרי אחד זה , אנו יכולים למפות אותו בחזרה למידות $ p $ עם $ \ mathbf V ^ \ top $. ואכן, יש למקם את הערכים של כל מחשב על אותו וקטור שבו שימש להקרנה; השווה את עלילות המשנה 1 ו- 3. התוצאה ניתנת על ידי $ \ hat {\ mathbf X} = \ mathbf {ZV} ^ \ top = \ mathbf {XVV} ^ \ top $. אני מציג אותו בעלילת המשנה השלישית לעיל. כדי לקבל את השחזור הסופי $ \ hat {\ mathbf X} _ \ text {raw} $, עלינו להוסיף את הווקטור הממוצע $ \ boldsymbol \ mu $ לזה:

$$ \ boxed {\ טקסט {שחזור PCA} = \ טקסט {ציוני מחשב} \ cdot \ text {Eigenvectors} ^ \ top + \ text {Mean}} $$

שים לב שאפשר לעבור ישירות מעלילת המשנה הראשונה לשלישית על ידי הכפלת $ \ mathbf X $ עם מטריצת $ \ mathbf {VV} ^ \ top $; זה נקרא מטריקס הקרנה . אם משתמשים בכל הווקטורים העצמיים $ p $, אז $ \ mathbf {VV} ^ \ top $ היא מטריצת הזהות (לא מבוצעת הפחתת מימדיות, ומכאן ש"שחזור "מושלם). אם משתמשים רק בקבוצת משנה של ווקטורים עצמיים, זה אינו זהות.

זה עובד עבור נקודה שרירותית $ \ mathbf z $ במרחב המחשב; ניתן למפות אותו למרחב המקורי באמצעות $ \ hat {\ mathbf x} = \ mathbf {zV} ^ \ top $.

השלכת (הסרה) של מחשבים מובילים

לפעמים רוצים להשליך (להסיר) אחד או כמה מהמחשבים המובילים ולשמור על השאר, במקום לשמור על המחשבים המובילים ולזרוק את השאר (כמו לעיל). במקרה זה כל הנוסחאות נשארות בדיוק אותו דבר , אך $ \ mathbf V $ צריך להיות מורכב מכל הצירים העיקריים למעט עבור אלה שרוצים להשליך. במילים אחרות, $ \ mathbf V $ צריך לכלול תמיד את כל המחשבים האישיים שרוצים לשמור.

אזהרה לגבי PCA בקורלציה

כאשר ה- PCA נעשה על מטריצת המתאם (ולא על מטריצת המשתנות), הנתונים הגולמיים $ \ mathbf X_ \ mathrm {raw} $ אינם מרוכזים רק על ידי חיסור $ \ boldsymbol \ mu $ אלא גם מוגדלים על ידי חלוקת כל עמודה לפי סטיית התקן $ \ sigma_i $. במקרה זה, כדי לשחזר את הנתונים המקוריים, צריך לשנות את קנה המידה של העמודות $ \ hat {\ mathbf X} $ עם $ \ sigma_i $ ורק אז להוסיף חזרה את הווקטור הממוצע $ \ boldsymbol \ mu $.

דוגמה לעיבוד תמונה

נושא זה עולה לעיתים קרובות בהקשר של עיבוד תמונה. שקול את Lenna - אחת התמונות הסטנדרטיות בספרות עיבוד תמונה (עקוב אחר הקישורים כדי למצוא מאיפה זה בא). למטה משמאל, אני מציג את הגרסה בגווני אפור לתמונה $ 512 \ פעמים 512 $ (קובץ זמין כאן).

נוכל להתייחס לתמונה בגווני אפור זו כ- $ 512 \ פעמים 512 $ מטריצת נתונים $ \ mathbf X_ \ text {raw} $. אני מבצע עליו PCA ומחשב $ \ hat {\ mathbf X} _ \ text {raw} $ באמצעות 50 המרכיבים העיקריים הראשונים. התוצאה מוצגת בצד ימין.

החזרת SVD

PCA קשור מאוד לפירוק ערך יחיד (SVD), ראה קשר בין SVD ו- PCA. כיצד להשתמש ב- SVD לביצוע PCA? לפרטים נוספים. אם $ n \ פעמים p $ מטריצה ​​$ \ mathbf X $ הוא SVD-ed כ- $ \ mathbf X = \ mathbf {USV} ^ \ top $ ואחד בוחר $ k $ - וקטור ממדי $ \ mathbf z $ המייצג הנקודה במרחב "U" המופחת "של ממדי $ k $, ואז כדי למפות אותה חזרה ל- $ p $ ממדים צריך להכפיל אותה עם $ \ mathbf S ^ \ phantom \ top_ {1: k, 1: k} \ mathbf V ^ \ top _ {:, 1: k} $.

דוגמאות ב- R, Matlab, Python ו- Stata

אני אנהל PCA על נתוני פישר איריס ואז בנה אותם מחדש באמצעות שני המרכיבים העיקריים הראשונים. אני עושה PCA על מטריצת השונות, ולא על מטריצת המתאם, כלומר אני לא משנה את המשתנים כאן. אבל אני עדיין צריך להוסיף את הממוצע בחזרה. חלק מהחבילות, כמו סטטה, דואגות לכך באמצעות התחביר הסטנדרטי. תודה ל- @StasK ו- @ Kodiologist על עזרתם בקוד.

נבדוק את השחזור של נקודת הנתונים הראשונה, שהיא:

  5.1 3.5 1.4 0.2  קוד> 

Matlab

  load fisheririsX = measure; mu = mean (X); [ ווקטורים עצמיים, ציונים] = pca (X); nComp = 2; Xhat = ציונים (:, 1: nComp) * וקטורים עצמיים (:, 1: nComp) '; Xhat = bsxfun (@plus, Xhat, mu); Xhat (1 , :)  

פלט:

  5.083 3.5174 1.4032 0.21353  

R

  X = iris [, 1: 4] mu = colMeans (X) Xpca = prcomp (X) nComp = 2Xhat = Xpca $ x [, 1 : nComp]% *% t (Xpca $ סיבוב [, 1: nComp]) Xhat = סולם (Xhat, center = -mu, scale = FALSE) Xhat [1,]  

פלט :

  Sepal.Length Sepal.Width Petal.Length Petal.Width 5.0830390 3.5174139 1.4032137 0.2135317  

לדוגמא R מעובדת לשחזור PCA של תמונות ראה גם תשובה זו.

פייתון

  ייבא מטומטם כ npimport sklearn.datasets, sklearn. decompositionX = sklearn.datasets.load_iris (). datamu = np.mean (X, axis = 0) pca = sklearn.decomposition.PCA () pca.fit (X) nComp = 2Xhat = np.dot (pca.transform (X ) [:,: nComp], pca.components _ [: nComp,:]) Xhat + = muprint (Xhat [0,])  

פלט:

  [5.08718247 3.51315614 1.4020428 0.21105556]  

שים לב שזה שונה מעט מהתוצאות בשפות אחרות. הסיבה לכך היא שגרסת פיתון למערך הנתונים של איריס מכילה טעויות.

סטאטה

  קשתית האינטרנט, clearpca sep * pet *, רכיבים (2) covariancepredict _seplen _sepwid _petlen _petwid, fitlist in 1 iris seplen sepwid petlen petwid _seplen _sepwid _petlen _petwid setosa 5.1 3.5 1.4 0.2 5.08303 3.5214. / code>